Walsh変換、フーリエ変換を用いた正規分布擬似乱数の生成手法

　Walsh transform (WT)  and Fourier transform (FT) generating normal/Gaussian distribution sequences

| ← back |
| home |


このページの内容は一般の方向けのものではありません．　新規に発見／再発見された、教科書には載っていない正規分布擬似乱数生成手法をご紹介しています．（大規模シミュレーション向けの効率的な手法と成り得る可能性がありますが、まだ詳細な評価・解析はおこなっていません）
一般の方はBox-Muller法や中心極限定理を応用した手法をご利用ください．

2025.6.12　Googleで『一様乱数をアダマール変換して正規乱数を発生させる方法』を検索したところ、下記のようなAIによる概要が表示されました．　２番目の検索例では、もっともらしい（？）Excelによる実装例まで表示されます．

　Gooleによる『一様乱数をアダマール変換して正規乱数を発生させる方法』のAIによる概要（その１）
　Gooleによる『一様乱数をアダマール変換して正規乱数を発生させる方法』のAIによる概要（その２）

　どのような資料を要約したのかは表示されませんし、なぜ正規分布擬似乱数になるのかも分かりません．　学習に用いた学術文献の記述内容を要約したのではなく、検索文字列に『一様乱数をアダマール変換』とあるので、単に一様乱数をアダマール変換する手順を答えたのではないかと思われます．

2025.5.8　参考文献として下記の資料を見つけました．　分かり易いWalsh変換の解説です．

　Walsh-Fourier Analysis and its Statistical Applications　David S. Stoffer, Journal of the American Statistical Association, June 1991, Vol.86, No.414

2025.4.13　関連文献として下記の資料を見つけました．　直交変換にこのような応用があるとは知りませんでした．

　直交変換による悪条件行列の改善法　小林 富士男, 福山大学工学部紀要 第10号, 89-95, 1988年3月
　DFTによる悪条件行列の改善　小林 富士男, 尾関 孝史, 筒本 和広, 福山大学工学部紀要 第30巻, 191-199, 2006年12月

2025.4.11　関連文献として下記の資料を見つけました．

　逆フーリエ変換を利用した任意スペクトルをもつ正規信号の発生　青島 伸治, 宮川 康彦, 計測自動制御学会論文集 15 (3), 389-394, 1979　PDFダウンロード

　著者名を見て、もしやと思って調べたら TSP(Time Streched Pulse)/ATSP(Aoshima's Time Stretched Pulse) の青島氏でした．

2025.4.8　先行文献として下記の資料を見つけました．　このような文献が今まで『埋もれていた』とは驚きです．

　アダマール変換を利用する多数の無相関な正規分布の不規則信号発生法　泉 照之, 計測自動制御学会論文集 27 (3), 365-367, 1991　PDFダウンロード

　上記文献に『一様乱数をアダマール変換して正規乱数を発生させる方法がある5)．』とありますが、参考文献の「5) 吉澤 正：Yatesの算法を応用した擬似正規乱数について、日本オペレーションズ・リサーチ学会研究会アブストラクト集、83/84 (1969)」に関する詳細情報はネット上には無いようです．　有償の科学技術文献複写サービスを利用するか、大学図書館・国会図書館等で調べるしかありません．（2025.4.9追記）
　参考文献 5) の著者名で調べると下記の情報がありました．　後者のコラムの末尾に『統計にはYatesの算法といわれるものが知られているが，詩人Yeatsと統計家Frank Yates（1902-1994）ではつづりが違うことがおもしろい』とあります．（2025.4.13追記）

　(株)日科技研：吉澤正先生がご逝去されました
　第41話 アイルランドの山の姿から —台地分布を考える—（六一学者の千字一話）

　Yatesの算法とは Yates analysis のことでしょうか？　他にYatesの業績とHadamard変換の関連についた述べた英文の情報がいくつかありますが、統計学の方面はまったく専門外なので良くわかりません．（2025.4.16追記）

　上記文献の中に「選点直交多項式」という用語が出てきますが懐かしい限りです．　東大の技官になった同級生のH君が無線関連の卒研で使っていた手法で、指導教官の先生は「選点直交関数を見つけてきて、その応用を考えたのはH君の功績だ」と話していたものです．

計測制御分野の古い関連文献を立て続けに２つ見つけましたが、時代背景として 計測用途の連続時間の試験信号をマイコンとD/Aコンバータを用いて生成する～という試みが活発におこなわれていたことが考えられます．　探せばまだまだ有用な文献をサルベージ出来るかもしれません．

概要
Walsh変換を用いた正規分布擬似乱数の生成（WT法）
フーリエ変換を用いた正規分布擬似乱数の生成（FT法）
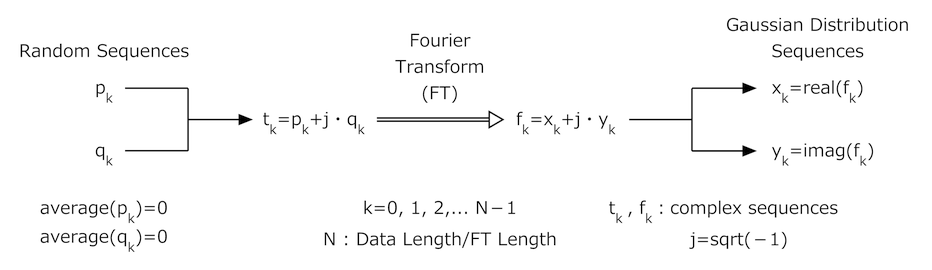
正規分布近似の基本原理
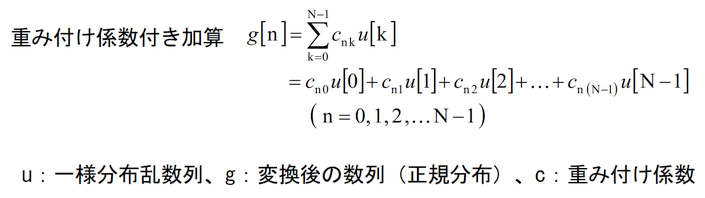
C言語のサンプル・プログラムとシミュレーション結果









Scilabのサンプル・プログラムとシミュレーション結果





上のグラフの形がかなり歪（左右非対称）に見えるので、一様分布乱数のseedを変えてもう一度プロットしてみました（2025.3.28追加）
（SEED='f0a50fa5', 'a5a53c3c', '0000ffff', 'ffff0000'）




一様乱数の代わりに-1/1の２値の擬似乱数を用いても正規分布乱数を生成できます．（2025/3/29追記）
左右のグラフは使用した２値の擬似乱数のseedが異なります．（Scilabプログラム pn_walsh_transform_method.sce）


















/* Gaussian random number sequence generator by FFT */
/* (c) 2025 cepstrum.co.jp                          */

clear;                                             // all clear
DATLEN=2^20;                                       // length=2^20=1048576
rand('uniform');                                   // set uniform random number mode 
rand('seed', hex2dec('a5a50f0f'));                 // set random number seed

//==========================================================================================
x=(rand(1:DATLEN)-0.5)+%i*(rand(1:DATLEN)-0.5);    // generate complex uniform random number
y=fft(x, -1);                                      // FFT
gauss_rand=[real(y), imag(y)];                     // complex ---> real conversion
//==========================================================================================

scf(0); clf;
plot2d(gauss_rand(1:3000), axesflag=1);

scf(1); clf;
histplot(-1500:50:1500, gauss_rand, axesflag=1);

savewave('out.wav', 0.9*gauss_rand/max(abs(gauss_rand)));






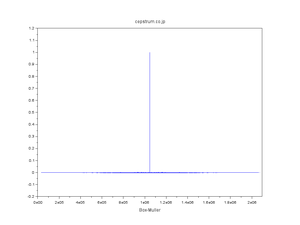
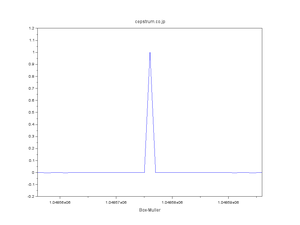
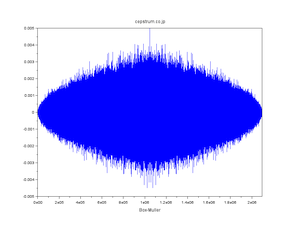
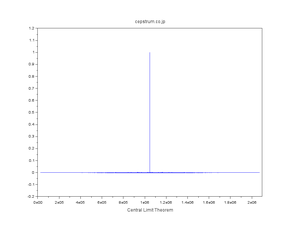
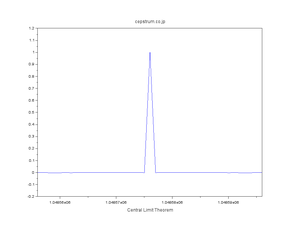
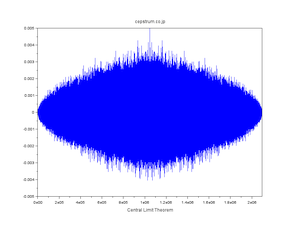
正規分布擬似乱数の自己相関
2025.4.7追加
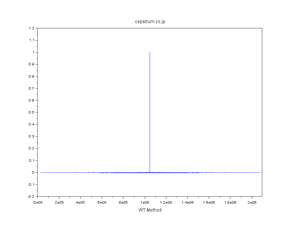
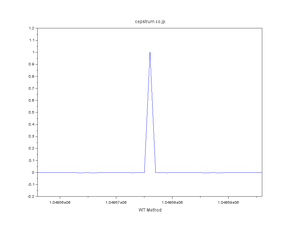
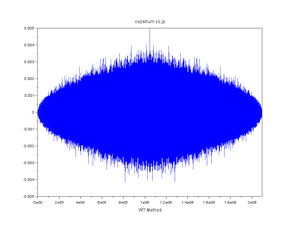
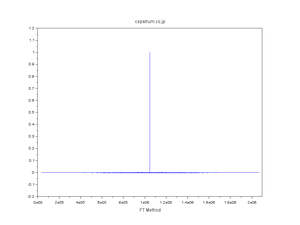
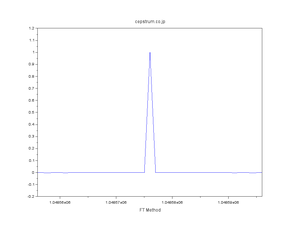
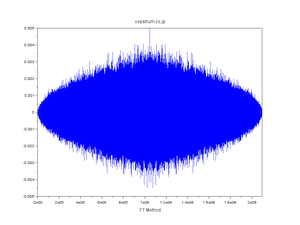
WT法・FT法・直交変換法 発見の経緯
FFTの使い方（電子科学シリーズ91）、安居院猛、中嶋正之、産報出版、1981（ISBNコードが日本で使われるようになる以前の本です）
FORTRANの算術型GOTO文／計算型GOTO文を目にしたのは何十年ぶりでしょうか. . . .
| ← back | ↑top |
 
| home |